Function VS Graph - 1

                                                                                     

  

  

ফাংশন কি আমরা সবাই জানি... যারা জানিনা তারা জেনে রাখি এটা একটা মেশিনের মতো যেখানে একটি ইনপুট দেওয়া হলে একটি আউটপুট বের হয়... যেমন ধান দিলে চাল বের হয় এরকম মনে করা যেতে পারে... 

যেমনঃ  যেখানে x দেওয়া হলে তার বর্গ ফাংশনটা রিটার্ন করবে...

 প্রায় সব জায়গাতেই ফাংশনকে গ্রাফের মাধ্যমে প্রকাশ করা হয়... ফাংশনের গ্রাফ আকার কিছু কিংবা কোনো ফাংশন দেখেই সেই ফাংশনের ধারণা গ্রাফ কেমন হতে পারে তার ধারণা পাওয়া যেতে পারে... গ্রাফিং ক্যালকুলেটর দিয়ে খুব সহজেই কোনো ফাংশনের গ্রাফ আকা গেলেও অনুধাবন করতে পারার আনন্দ নেই... ইন্টুইশন এর মাধ্যমে একদম বেসিক এক ঘাতের ফাংশন থেকে সূচকীয় কিংবা লগারিদমীয় ফাংশনের গ্রাফ কেমন হতে পারে ধারণা করা যায় (হ্যা ধারণা করা যায়, কারণ সব ফাংশনের গ্রাফ এক্সেক্টলি হাতে আকা সম্ভব নয়)... আর ধারণা থেকে গ্রাফ করতে পারাটা গুরুত্বপূর্ণ... ধীরে ধীরে সবই আসবে...

আর্টিকেলের সকল গ্রাফের চিত্র Desmos থেকে নেয়া হয়েছে... অন্যান্য অনেক গ্রাফিং ক্যালকুলেটর থাকলেও, এটা ব্যবহার করা সবচেয়ে সহজ, আর দেখতেও সুন্দর। যদি Desmos এপ না থেকে থাকে তাহলে প্লেস্টোর থেকে ডাউনলোড করে নাও...

শুরু করি দুনিয়ার সব থেকে সহজ ফাংশন দিয়ে (এটা কি আদো ফাংশন ?) 

                                                                        

                          এই ফাংশনের গ্রাফ কি হবে? y অক্ষ বরাবর ফাংশন হলে, x যত y ওহ তত নাহ?   

                                   

হুম, মোটামুটি এই ফাংশনের গ্রাফ থেকেই অনেক ধরণের ফাংশনের গ্রাফের ধারণা পাওয়া যায়... যেমন?

তুমি উপরের গ্রাফ জান... তবে কি   ফাংশনের গ্রাফ কেমন হবে আন্দাজ করতে পারো? ভাবো...

আগে x এর জন্য y এর যে মান পাওয়া যেত, এখন x এর সেই মানের জন্য y এর মান 5 বেশি পাওয়া যাবে না? অর্থাৎ x এর আগের মানের চেয়ে 5 কম মানের জন্য নতুন ফাংশনের y এর একই (পূর্বের ফাংশনের সমান) মান পাওয়া যাবে... তাই না? তাহলে নতুন ফাংশনটি কেমন হবে? আগের ফাংশনের সরলরেখাটি 5 ঘর বামে সরে যাবে না? হুম... দেখো তো...

        

                 

বুঝে থাকলে  এর গ্রাফ মুহুর্তের মাঝেই কল্পনা করোতো...

আচ্ছা আবার প্রথম গ্রাফে ফিরে আসি... যদি   হয় তাহলে এর গ্রাফ কেমন হবে? পরমমানের জন্য

x  অক্ষের ঋণাত্মক অংশের জন্য y এর মান ধনাত্মক হয়ে যাবে না? অর্থাৎ y এর ঋণাত্মক অংশ ধণাত্মক হয়ে যাবে, উপরে উঠে আসবে, দেখে মনে হবে যেন প্রতিফলন হয়েছে...      

                                                                                        

                

  

এতটুকুবোঝা শেষ? তাহলে   গ্রাফ কেমন হবে? ধাপে ধাপে চিন্তা করো...

আচ্ছা  আর   কি আসলে একই জিনিস নাকি ভিন্ন? ভাবো...  একই তো হওয়ার কথা... উভয় ফাংশনেই দেখা যাচ্ছে ধণাত্মক x এর সাথে শুধু 5 যোগ...

না একই নয়... প্রথম ফাংশন আগেই ব্যাখ্যা করা হয়েছে, পুরোটাতে পরমমান থাকায় x + 5 এর গ্রাফের যে অংশে y এর মান ঋণাত্মক পরমমানের জন্য সেই নিচের অংশটুকু উপরে উঠে আসবে... কিন্তু, দ্বিতীয় ফাংশনে শুরুতে x এর পরমমান নেওয়া হয়েছে, এখানে ফাংশন চেঞ্জ অলরেডি একবার হয়ে গিয়েছে, অর্থাৎ রেঞ্জের পরিবর্তন হয়ে গেছে। এরপরের যোগ করা 5 এর জন্য পরিবর্তিত ফাংশনের প্রতিবার ৫ বেড়ে যাবে না? ফাংশনের মান ৫ বেড়ে যাওয়া মানে কি? ফাংশনে পূর্বের মানের চেয়ে একই ডোমেইনে ৫ বেশি মান পাওয়া যাবে... তারমানে, পরমমান হওয়ার পর সম্পূর্ণ অংশটুকু y অক্ষের দিকে ৫ ঘর উপরে উঠে যাবে না? 

   

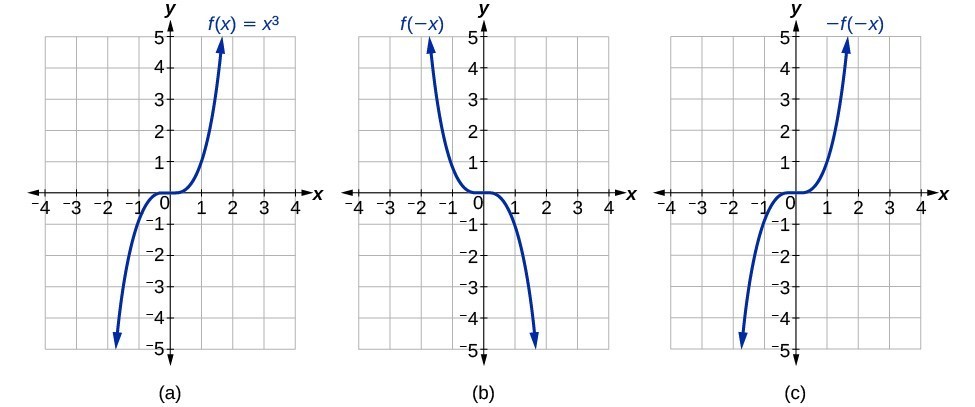
গ্রাফ দেখে আন্দাজ করতো কোনটা কোন ফাংশনের গ্রাফ? এখন  এবং   ফাংশনের গ্রাফ জলদি বের করে ফেলতো...

এতক্ষণ তো শুধু যোগ বিয়োগ করলাম... তাহলে   গ্রাফ কেমন হবে? আমাদের সেই বেস ফাংশনের সাথে তুলনা করলে কি দাড়ায়? পূর্বের থেকে দ্বিগুন মান আসবে... তারমানে হলো পূর্বের গ্রাফের সরল রেখাটা y অক্ষের দিকে হেলে যাবে। ২ গুণ হেলে যাবে...

      

আচ্ছা  এর গ্রাফ কেমন হবে ? ২ গুণ করার পর ৫ বেড়ে গিয়েছে... বেড়ে গেলে কোন দিকে যাবে? y অক্ষের দিকে না? হুম, 2x এর গ্রাফ ৫ ঘর উপরে উঠে যাবে... নিজে নিজে এমন কয়েকটা ফাংশন লিখে আনুমানিক গ্রাফ আকতে থাকো...

আজ এই পর্যন্তই, আগামীতে ধীরে ধীরে দ্বিঘাত, ত্রিঘাত, ত্রিকোনোমিতিক, সূচকীয়, লগারদিমীয় ফাংশন নিয়ে আলোচনা করবো...